特に「小数のかけ算」「小数のわり算」はつまずきやすい単元の一つ。
ここでのつまずきは後々算数への苦手意識に大きく影響しますので、少しの困り事も見逃さないでいただきたいですね。 しかしお子さんにいざ小数を教えようと思うと、
「なぜ小数点が移動するんだっけ?」
「小数の文章問題をわかりやすく説明できない……」
と、おうちの方も混乱する場合が多いようです。
本記事ではそうしたお悩みに向けて、「小数の教え方の3つのポイント」を分かりやすく解説しました。
小数のかけ算や小数のわり算の教え方でお困りの方は、ぜひ最後までお読みください。
目次
小数のけけ算・わり算の教え方の「3つのポイント」
小数のかけ算・わり算や小数点の教え方には、3つのポイントがあります。
- 小数の理解は低学年の復習から!
- 小数の計算は「小数点の位置」が重要
- 小数のかけ算・わり算で小数点が移動する理由を教えよう!
それぞれ詳しく解説していきます。
※「小学生の算数でつまずきやすいポイント」についてはこちらの記事で詳しく解説しています。
小学生の算数について大枠を掴みたい方はぜひご一読ください。
1. 小数は低学年の「十進法」から復習スタート!
小数の学習は、低学年の算数が密接に関わっています。
中・高学年の算数でつまずいているお子さんは、低学年の内容でつまずいているケースが多く見られます。
特に「10のまとまりが10個で100」という十進法の概念の理解が重要なカギになります。
「1を10等分すると0.1」「0.1が10個で1」を理解できないと、お子さんは小数の学習を難しく感じてしまうのです。
まずは、お子さんのつまずき具合を確かめて、復習してみましょう。
場合によっては学年を遡って復習する必要があります。
「【小学生】算数の計算ミスがなくならない!7つの原因と対策方法を徹底解説(学び相談室)」
実はとても重要である十進法(小3)
「10が10個で100」「100が10個で1000」というように、10のまとまりで位が変わる十進法をお子さんはこれまでに学習してきています。
小数はその逆で、ある単位(1)を10等分して新たな単位(0.1)をつくり、「その単位がいくつぶんか」を数の大きさや小数点の位置で表しています。
例えば、「1㎏を10等分すると0.1㎏で、それが4つ分で0.4㎏」「1㎝を10等分すると0.1㎝で、それが7つ分で0.7㎝」と表します。
このように、1より小さい数を表すのが小数です。
端数を理解する (小3)
小数のよさは「端数(はすう)」を表せることです。
端数という言葉の意味は子どもにとって難しいですが、「少し余ってしまった部分」と教えるとよいです。
世の中にはピッタリの数字で表せない数字があります。
例えば体重。
「体重42㎏700g」という数字を見て違和感を感じる人は多いでしょう。
「体重43.7㎏」と表した方が短く、わかりやすいです。
大人は「端数は小数で表した方がよいこと」を理解しています。
まずは、端数の部分は小数で表すよさをお子さんに気づかせていきたいですね。
また、子どもにとって小数はとても複雑かつ抽象的な概念です。
「小学4年生から算数が難しくなった」という言葉をよく耳にしますが、それは抽象的な内容が増えるからです。
そこで、低学年の学習と同じように、具体物(図)を使って教えるとよいでしょう。
(小学校低学年では、おはじきや計算タイルなどをよく使いますね)
小数の学習でおすすめの具体物は「1Lの計量カップ」です。
0.1L(100mL)ごとに目盛りがついているので「1(L)より小さい数」を理解しやすいです。
「1L600mLが1.6Lである」と、端数も計量カップを使うことで理解しやすくなります。
「~を1とみる」という「基準量」の考え方 (小4)
小学5・6年生になると、「割合」「平均」を学習するので、小数で答えを表す場面が増えます。
そこで重要になる考え方が「~を1とみる」という基準量(もとの数)の考え方です。
例えば、「4を1とみると6は1.5にあたる(1.5倍)」「15を1とみると54は3.6にあたる(3.6倍)」といった感じです。
そして、ここでもう一つお子さんに理解させたいのは、1.5倍や3.6倍といったように「小数は倍を表す場合があること(小数倍)」です。
このように、2年生で学習したかけ算は、小数が加わってさらに広がっていきます。
お子さんは低学年で学習した内容を拡張させながら小数を学んでいくのです。
ですから、低学年の学習を理解していないと、小数の学習でつまずく(あるいは、つまずいている)可能性があります。
今一度、お子さんのつまずき具合や学習の定着度を確認してみましょう。
2. 小数の計算は「小数点の位置」をしっかり理解する
小数の計算でやっかいな点が「小数点の位置」。
実は小数の計算は、基本的に整数の四則計算(たし算、ひき算、かけ算、わり算)と同じです。
「えっ?! 整数の計算と同じ?」と不思議に思う人もいるかもしれません。
しかし四則計算のルールを整数で理解していれば、「小数点の位置はどこ?」という問題は容易に解決できるのです。
小数のたし算・ひき算は「小数点をそろえる」(小3)
たし算・ひき算は「位をそろえて計算する」が絶対ルールです。
「位をそろえる=小数点の位置をそろえる」を徹底しましょう。
例えば、7.5+2.4であれば、

34.2+2.83であれば、

整数のたし算・ひき算のひっ算をマスターしていれば、小数のたし算・ひき算はほとんどクリアできます。
小数のかけ算・わり算は簡単な計算から(小4)
小数のかけ算・わり算は、
①「小数×(÷)整数」
②「整数×(÷)小数」
③「小数×(÷)小数」
の3パターンのみです。
小学4年生では「小数×(÷)整数」の学習をします。
「整数×(÷)小数」「小数×(÷)小数」は小学5年生の学習です。
まずは2.4×5や4.7×8といった「小数×(÷)整数」の計算から始めましょう。
小数のかけ算・わり算で問題になってくるのは「小数点の移動」です。
多くのお子さん、親御さんが頭を悩ませています。
具体的なポイントや教え方は記事の後半で詳しく解説していきます。
問題を図式化して計算しよう
小数の計算方法の他に、もう一つ重要なポイントがあります。
それは、問題文を図式化する力です。
「8人に4Lのジュースを等しく分けると1人何リットル?」という問題ができない小学6年生が半数近くの割合でいることが、話題になりました。
(参考:小6の43%が誤答「8人に4Lのジュースを等しく分けると1人何リットル?」迷いなく8÷4と立式する子への教え方)
小数のかけ算・わり算では、計算力だけでなく「問題文から立式(式を立てる)すること」も重要です。
立式できなければ、計算を始められません。
立式するためには、問題文を読んで図や表をイメージしたり書き起こしたりする力が必要になります。
問題文を図式化する(図に表して式にする)力もお子さんに意識させていきたいです。
先ほどの「8人に4Lのジュースを等しく分けると1人何リットル?」という問題を図に表してみましょう。
図にすると式が考えやすくなりますね。
「4Lを8人に分けて、1人何Lになるか?」「式は4÷8であること」がよくわかります。
また、問題文を図式化すると答えは4より小さくなるという見当もつき、誤答を防げます。
誤答として多いのが「8÷4」と式を立ててしまい、答えを2(L)としてしまうパターン。
図をイメージできれば、
「1人分が2Lだと、16Lあることにならない? おかしくないか?」という感じで、誤答に気づけます。
(正解は4÷8=0.5Lで、1人分は0.5L)
計算はできるが、問題から式を立てられないためにテストの点数が伸びない子は高学年から目立ち始めます。
お子さんが計算力はあるのに文章問題が苦手、とお悩みのおうちの方は多いと思います。
小学3・4年生以降の算数では、問題(抽象的なお話)を図式化する(具体的にする)習慣を身につけることをおすすめします。
3.小数のかけ算・わり算で小数点が移動する理由を教えよう!
ここからは、小数のかけ算・わり算の小数点が移動する理由を解説していきます。
お子さんの「なんで小数点が移動するの?」という質問に、堂々と答えられるようになりましょう。
ポイントは2つです。
- (数が小さい、小数点の移動が少ない)簡単な式から教える
- 「計算方法のしくみ(意味)」と、「ひっ算のやり方(方法)」を分けて理解させる
小数のかけ算のひっ算
12×4.3(整数×小数)の式を例に考えましょう。
小数のかけ算は整数のかけ算にするのがポイントです。
①12×4.3の4.3を10倍(×10)して、12×43にする
(なぜ12×43にするのか? 整数×整数は学習済みだから)
②12×43=516
しかし、516は12×4.3の答えではない……
元の式(12×4.3)を10倍(×10)したのだから、元に戻す!
元にもどすには、答えの516を10で割る(÷10)
③516÷10=51.6
ひっ算の形で解いてみてください。
①〜③の手順で計算しているはずです。
このように、「なぜ小数点が移動するのか?」の意味がわかれば、ひっ算の方法も理解できます。
そして、小数を整数にする時、
「10倍すると小数点は右へ1ケタ移動する。100倍すると小数点は右へ2ケタ移動する」
「10で割ると小数点は左へ1ケタ移動する。100で割ると小数点は左へ2ケタ移動する」
というルールは必ず押さえましょう。
12.3×2.7(小数×小数)の式で考えてみましょう。
①1.23×2.7の1.23を100倍(小数点は右へ2ケタ移動)、2.7を10倍(小数点は右へ1ケタ移動)して、123×27という整数の式にします。
100倍と10倍をしているので、全体で1000倍(小数点は右へ3ケタ移動)していることになります)
②123×27=3321
1.23×2.7の式を1000倍しているので、3321を1000で割る(小数点が左へ3ケタ移動)
③3321÷1000=3.321
ひっ算でも試してみてください!
小数のわり算のひっ算
わり算には次のようなルールがあります。
「わられる数、わる数に同じ数をかけても、同じ数で割っても商(答え)は変わらない」
整数のわり算で説明してみます。
24÷8=3です。
ここから、わられる数の24とわる数の8に同じ数の10をかけて、240÷80にして計算すると答えはいくつでしょう?
240÷80=3となり、24÷8の答えと変わりません。
このわり算のルールを、小数のわり算で活用します。
では、48÷1.2(整数÷小数)で考えてみましょう。
①48÷1.2の48と1.2の両方を10倍して480÷12にする
②480÷12=40
③先ほどのわり算のルールから、答えの40は48÷1.2の答えと同じになります
小数のわり算は①〜③の手順に沿っています。
確かめてみてください。
5.94÷4.5(小数÷小数)で考えてみましょう。
①5.94÷4.5の5.94と4.5の両方を10倍して、59.4÷45にします
②59.4÷45=1.32
③わり算のきまりから、答えの1.32は5.94÷4.5の答えと同じ
ちなみに、5.94÷4.5の5.94と4.5の両方を100倍して、594÷450にしても答えは1.32になります。
ここで「10倍にしたらいいの?100倍にしたらいいの?」という新たな問題が発生します。
答えは「わる数を整数にすればOK」です。
理由はひっ算の形にするとわかります。
わる数の4.5を100倍や1000倍にして450、4500にすると、書きにくくなります。
4.5という数字を書き直す手間がかかります。
ですから、5.94÷4.5の場合はわる数の4.5が整数になればよいので、10倍にします。
わり算のひっ算でわる数の小数点から移動するのは、そのためです。
ひっ算も試してみてくださいね。
小数点のポイントは、整数の計算に「するとき」や「もどすとき」
小数のかけ算・わり算で起こる小数点の移動は、整数の計算にしたり、元の式にもどしたりする時に発生します。
小数点がただ移動しているのではなく、かけ算やわり算の計算のルールに沿って移動しているのです。
つまり、算数は四則計算のルールの一つ一つを確実に理解することが重要です。
計算ができるだけでなく、「なぜこの計算方法ができるのか?」を考えられると算数の力は飛躍的にアップします。
確実な理解のためには復習が重要です。
特に今回の小数の計算の場合は、整数の計算、かけ算やわり算のルールといった以前学習した内容を理解していれば、つまずきは小さくなります。
ぜひ復習を大切にしてください。
「RISU算数」なら小数のかけ算わり算を基礎から復習できる

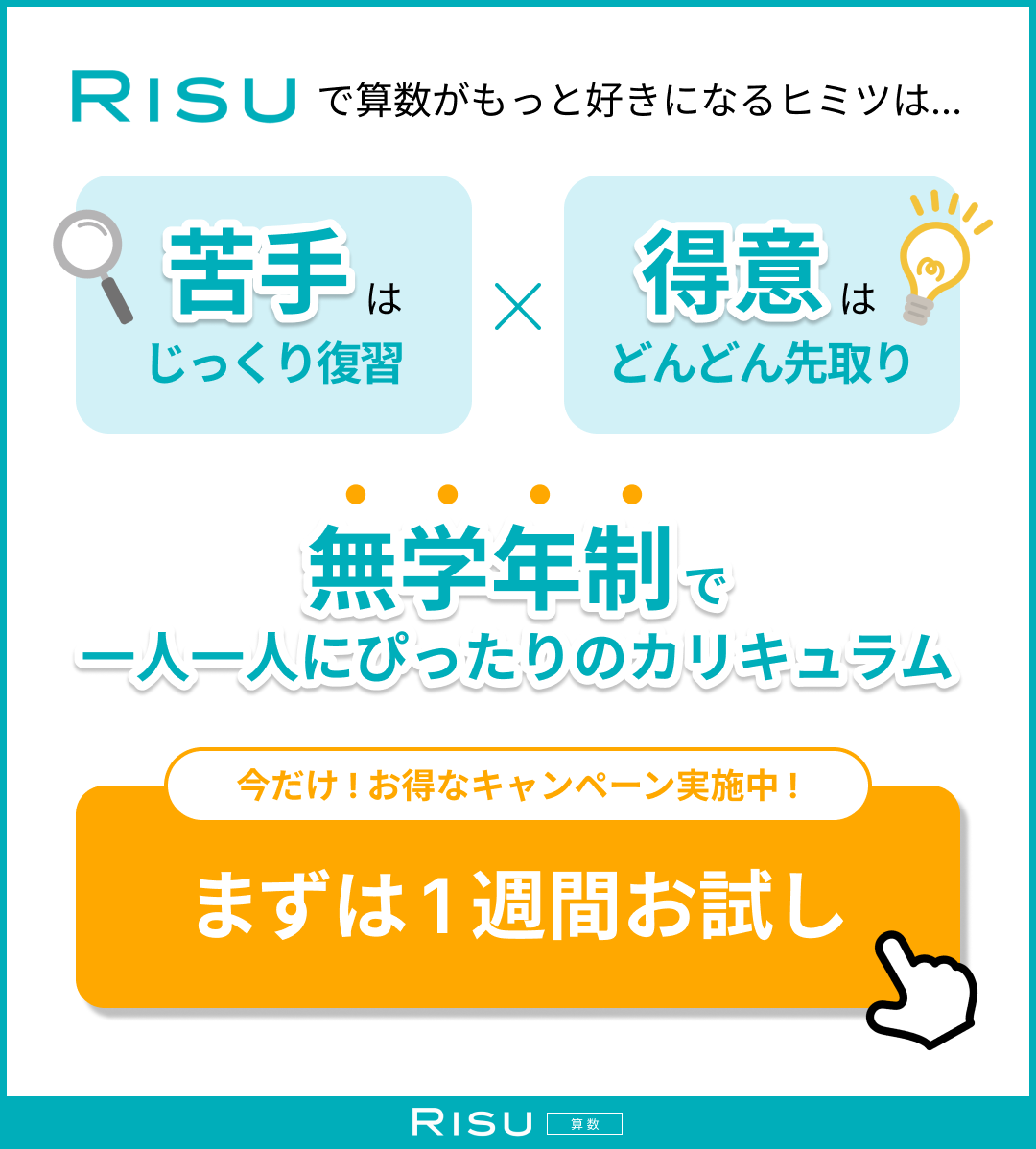
算数専用タブレット教材の「RISU算数」は、学習習慣が自然に身につく機能が豊富。
おうちの方が「勉強しなさい」と言う必要が無くなった、というお声をたくさんいただいています。
勉強が難しくなる小学校高学年は、親子の距離感も難しい時期。
お子様が自立して学べる機能が豊富なRISU算数をぜひお試しください。
つまずきなく着実に算数力が身に付くRISU算数の3つの特長をご説明します。
1.スモールステップ&無学年制カリキュラム
4歳から中学受験基礎(さらに中学数学基礎)の問題まで約10000問を収録。
スモールステップで少しずつ先に進むので、つまずきにくく自然にステップアップしていけます。
またRISU独自の無学年制カリキュラムを採用。
学年を超えてどんどん先取り学習を進めることも、つまずいた分野では学年を遡って復習することもタブレット一台で完結します。
紙のテキストのように何学年分も用意する必要はありません。
また「算数検定マスター判定」によって、算数検定の受検可能級をお知らせ。
実際より上の算数検定の階級に合格することで、受検費用が0円になるおトクなサポート制度もあります。
先取り学習の定着度や分野別の得意不得意の分析に算数検定を活用できます。
参照サイト:RISU算数が算数検定対策になる!助成金で検定料を無料にする方法も解説
2.データ分析で一人ひとりにベストな問題が届く
RISU算数では、タブレットを通じて利用者ひとりひとりの学習データを常に収集・分析。
得意分野・苦手分野を把握し、利用者の実力に合った問題となるよう、お子様に合わせて問題が変わっていきます。
難しすぎてついていけなくなったり、簡単すぎて飽きてしまうこともないのです。
一人ひとりのペースに合わせて、効率よく実力を伸ばすことができるのがRISU算数の大きな特長です。
ほかにもお子さんにもおうちの方にも嬉しい機能がたくさん。
くわしくはこちらをご覧ください。
3.自動採点機能つき ゲーム感覚でどんどん進む
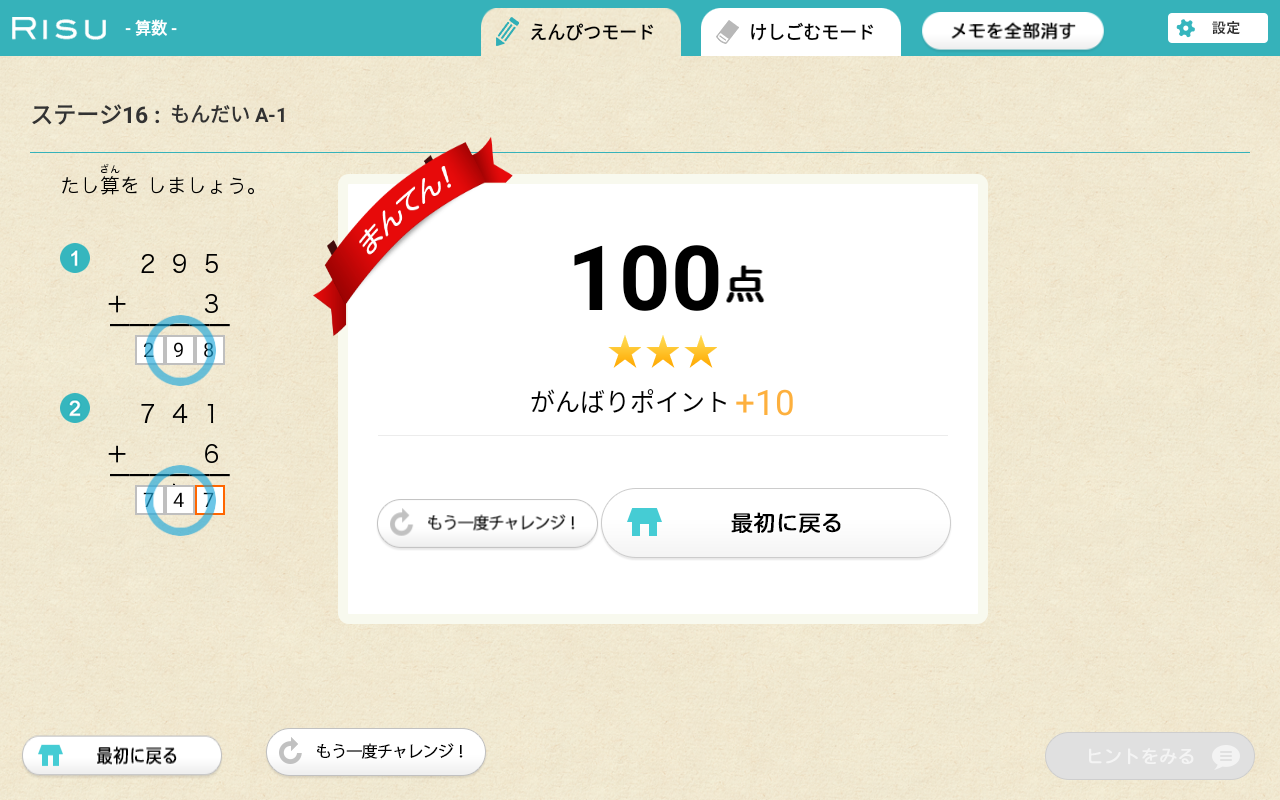
タブレット教材のRISU算数なら問題を解いたら自動採点機能でその場ですぐに採点。
おうちの方が丸つけする必要がないので、お子さんだけでどんどん学習をすすめることができます。
テンポよくステージをクリアしていくことで、まるでゲームを攻略するように楽しんで進めることができます。
RISUのタブレット教材ならば飽きることなく、楽しく学習できます。
また、忘れてしまいがちなタイミングでの復習と間違いが多かった問題の復習をミックスして復習を自動出題し、学習の定着を図れます。
さらに、つまづきを感知してフォローアップし、やる気や学習習慣づけまでサポートしてくれます。
親御さんが細かく口を出す必要が無いので、親子の丁度いい距離感を保つことができます。
RISU算数を活用した中学受験のリアルな体験談はこちらの記事で詳しくご紹介しています。
RISU算数を中学受験に徹底活用!入塾準備から志望校合格までリアルな体験談をご紹介
まとめ:小数のかけ算・わり算は「算数が得意or苦手」の分かれ道
小数は高学年の本格的な算数の土台となる重要単元。
小数の計算や小数の文章問題でのつまずきをきっかけに、算数が苦手教科になってしまうお子さんは非常に多いです。
算数は積み上げの教科ですから、ちょっとのつまずきをスルーしてしまうと、必ず後々のつまずきの原因となります。
お子さんが少しでも小数に困ってしまっている様子が見られたら、ぜひ本記事を家庭学習の参考にされてみてくださいね。
RISU利用者レビューでは、RISU算数をご利用いただいている保護者様の声をご紹介しています。
中学受験で志望校合格、大手塾模試で成績が大幅アップ、家庭学習の質が上がった、など皆様の参考になるリアルな体験談が多数。
RISU公式ブログでは、算数オリンピックメダリストや先取り学習での算数検定合格者、大手塾主催模試での成績優秀者など、お子様の声を中心にご紹介しています。
ぜひ一度お読みください!
RISU算数の効果や料金を紹介┃利用者の評判はどう?(おもすく)