小2では、簡単な分数の足し算・引き算と、「分ける」という概念を学習します。
小3からより本格的な分数の学習に入り、小4・小5では分数の足し算・引き算を学習していきます。
小6では分数の掛け算・割り算を学習し、いろいろな単元に分数が登場します。
今回は小学校で学習する分数の内容を詳しく解説します。
お子さんがつまずいているポイントを発見したり、見通しをもって先取り学習をしたりするための参考にしてください。
小2・小3で学習する分数
分数の学習は小2から登場します。
小2・小3で学習する分数は、分数の基礎となる部分です。
高学年以降の分数を使った複雑な文章問題のための土台となる重要な時期ですの、一つ一つ丁寧に納得しながら学習を進めていきましょう。
「分数が理解できない原因は？つまずくポイントと対策を詳しく知りたい（学び相談室）」
【小2】ものを「分ける」を学習
小2の学習では、身の回りの物を題材に1/2や1/4、1/8といった簡単な分数を作ります。
例えば、折り紙を半分に折って1/2、もう一度半分に折って1/4、さらにもう一度半分に折って1/8というように、目で見て理解しやすい分数を学習します。
また、チョコレート12個の1/2は6個、1/3は4個といったような「分ける」学習もあり、小3で学習する割り算の素地を作る狙いもあります。
さらに小2では、「12個の1/2は6個⇒12個は6個の2倍」「12個の1/3は4個⇒12個は4個の3倍」といったように、掛け算・割り算の関連性にも触れていきます。
【小3】分数の意味と表し方・簡単な足し算と引き算を学習
小3では、まず分母と分子のといった用語を学習します。
また1/2や1/5といった分子が1である単位分数を学習します。
分数には大きく5つの意味がありますが、小3では次の3つの意味を学習します。
①具体物を等分したうちのいくつ分の大きさ
例 ケーキを6等分したうちの5つ分は⅚
②測定した量の大きさ
例 2/3mL
③1を等分したもののいくつ分の大きさ
例 1を5等分したうちの3つ分は⅗
小3の分数では、整数の学習と同じように分数で大きさを比較したり、簡単な足し算・引き算を学習します。
足し算や引き算は、1/5＋2/5や6/7-3/7といった同じ分母同士（同分母）の計算をします。
【小2・小3のポイント】具体的な分数のイメージを育てよう
小2・小3は、実際に物を使って、視覚的に分数のイメージをもつことが重要です。
折り紙などの物を半分にする作業や、1/4にあたる部分に色を塗ったりし、感覚的に分数を理解させていくとよいです。
小3からは割り算の学習も始まるので、物を分ける作業をやりながら分数を学ぶと、割り算と分数のつながりを感じやすくなります。
「小３の子どもへの分数の教え方を知りたい！家庭で簡単にできる方法はありますか？（学び相談室）」
小4・小5で学習する分数
小4では1より大きい分数を学習し、小3で学習した分数が広がっていきます。
小5では通分や約分、分母が異なる足し算・引き算といったお子さんがつまずきやすい内容が登場します。
また、5つの分数の意味のうち、残りの2つを小5で学習します。
④Bを１としたときのAの割合
⑤整数の割り算の結果
1÷3=1/3
【小4】真分数・仮分数・帯分数を学習
小3までは1/2や5/8、9/12などの1より小さい分数を学習してきましたが、1より大きい分数を小4で学習します。
3種類の分数、真分数、仮分数、帯分数の違いや計算について習います。
- 真分数（しんぶんすう）・・・1/2や3/5など、分子が分母より小さい分数。
- 仮分数（かぶんすう）・・・3/2、4/4、20/8など、分子が分母以上（分母より大きいか等しい）の分数。
- 帯分数（たいぶんすう）・・・1½、3¼など、 整数と真分数の和で表される分数。
分数の足し算・引き算も１より大きい分数が答えになり、「仮分数で計算する方法」と「帯分数で計算する方法」を学習します。
ここでは仮分数を帯分数に、帯分数を仮分数に変換できるようにすることが重要です。
分数の変換は小5・小6の算数に大きく関わってくるからです。
下の図のように、分数の足し算・引き算は帯分数で計算した方が整数と分数の区別がついた状態で計算できます。
一方で、分数の掛け算・割り算は仮分数で計算した方がやりやすいです。
途中で約分をしやすくなるからです。
途中で約分をせずに計算すると、大きい数字の答え（上の図の場合は200/30）を約分することになります。
仮分数と帯分数の意味や変換のやり方を小4では確実に理解しましょう。
また、小4では1/2＝2/4というように、大きさの等しい分数も学習します。
これは、通分の学習につながっていきます。
【小5】通分・約分を学習
小5の分数では、通分と約分が登場します。
異分母の足し算・引き算では、分母を同じにする通分をしてから計算します。
2/5＋1/3＝6/15＋5/15＝11/15
通分をするためには、小2で学習する九九の理解と、小5で学習する公倍数や最小公倍数の理解が重要です。
3と5の公倍数
15、30、45、60・・・
最小公倍数は15
また、計算で求めた答えの分母を最も小さくする約分は、お子さんがつまずきやすい箇所です。
4/12⇒1/3 36/96⇒12/32⇒3/8
約分は、九九はもちろんのこと、小3で学習する簡単な割り算の理解が大きく関わっています。
公約数や最大公約数の理解も必要です。
例えば、24と32の公約数は、
24の約数
1 2 3 4 6 8 12 24
32の約数
1 2 4 8 16 32
同じ約数が公約数だから、
1 2 4 8
が24と32の公約数で、8が最大公約数となります。
約分をする際には、分子と分母の両方を割れる数（公約数）を見つけるのがポイントになります。
小5ではさらに、分数と整数・小数の関係も学習します。
a＝a/1
3=3/1
0.13＝13/100
1/4=1÷4=0.25
この学習により、これまで割り算で割り切れなかった答えを分数で表すことができるようになります。
1÷3＝0.333・・・
1÷3=1/3
【小5】「割合」を学習
小5では割合の学習があり、ここでも分数が登場します。
次のような問題を考えてみましょう。
「Aさんはシュート12本中7本成功しました。Bさんはシュート9本中5本成功しました。どちらがより多く成功したといえますか？」
この問題はシュート1本あたりの成功数といった単位量あたりの大きさを求めますが、分数でも求められます。
A 7/12 B 5/9
しかし、これでは分母（シュート数）が異なるため、比較ができません。
そこで通分をします。
A 7/12⇒21/36 B 5/9⇒20/36
分母（シュート数）を同じにするとAさんの方がより多く成功したといえます。
そして、問題のたびに通分して解くのは大変だから、他のよりよい求め方を考えていく流れに小学校ではなります。
そこで割合が登場。
先ほどのAさんの7/12は、7÷12＝0.5833・・・となります。
これはシュート1本あたりの成功率を表しており、百分率にすると58.3％です。
このように、割合の学習は分数が起点となっています。
小6で学習する分数
最終学年の小6では、つまずきが多いといわれる分数の掛け算・割り算が登場します。
【小6】分数の掛け算・割り算を学習
分数の掛け算・割り算は四則計算の総まとめです。
これまで学習してきた九九、通分・約分をフル活用して計算します。
分数の掛け算・割り算では、九九と約分がポイントです。
特に約分は、小5で学習する足し算・引き算でもお子さんの悩みの種になりやすく、苦手意識が小6にも引き継がれます。
上の図は約分でつまずく例です。
①でつまずいているお子さんは小5で学習する約数の復習が必要です。
場合によっては、九九の復習が必要かもしれません。
②と③は、約分のやり忘れで減点されるケアレスミスのパターンで、算数が得意なお子さんでも起こりえるミスです。
例えば、計算の答えが24/36だったとしましょう。
24と36の約数である3で約分をすると、8/12になります。
この一度の約分で「よし約分できた！」と満足して計算が終わるお子さんは多いです。
8/12はまだ4で約分でき、2/3にできます。
よりベターな解法としては、24と36の最大公約数である12で約分し、2/3に導けるのがよいです。
このように、分数の掛け算・割り算は九九や公約数の理解が不足しているとつまずきやすい単元で、約分の有無に気付く力の差となります。
【小6】比、反比例、単位量あたりの大きさを学習
小6では、以下の単元で分数が出てきます。
- 比 2：3＝2/3（比の値）
- 反比例 一方が2倍、3倍・・・、もう一方が1/2、1/3の関係
- 単位量あたりの大きさ
中でもお子さんが苦戦しやすいのが、単位量あたりの大きさ。
例えば、「1m120円のテープの4/5ｍ分の値段を求める」という問題があったとしましょう。
120×4/5で求められますが、「なぜ4/5をかけるのか？」「そもそも分数をかけてよいのか？」を小学校の授業では考えていきます。
分数のイメージができていないお子さんは、120÷4/5としてしまいがちです。
そもそも、分数を掛けることは子どもからするとなかなか理解しがたいものです。
こうした抽象的な内容が小6や中学校の数学では増えていきますので、小2から分数を視覚的に理解し、数をイメージした学びが大切です。
「RISU算数」なら分数をイメージしながら学べる
算数の家庭学習には、算数専用タブレット教材の「RISU算数（幼児には「RISUきっず」）」がぴったりです。
タブレット学習ならではの視覚的な学びによって、抽象的になりがちが分数もイメージを捉えることができます。
RISU算数の特長3つをご紹介します。
特長1：「無学年制」で一人ひとりにピッタリのカリキュラム
RISU算数では無学年制カリキュラムを採用。
学年を超えてどんどん先取り学習を進めることも、
つまずいた分野で学年を遡って復習することもタブレット一台で完結します。
またRISU算数ではデータに基づき、お子様の学力に合わせた出題がなされるため、
難しすぎて勉強が嫌いになってしまうということや、簡単すぎて退屈するということもありません。
つまり、解き甲斐があり楽しい問題がつづくため学習習慣が自然に身につき、着実に基礎力を固めることができるのです。
特長2：文章問題・図形問題で思考力が身に付く
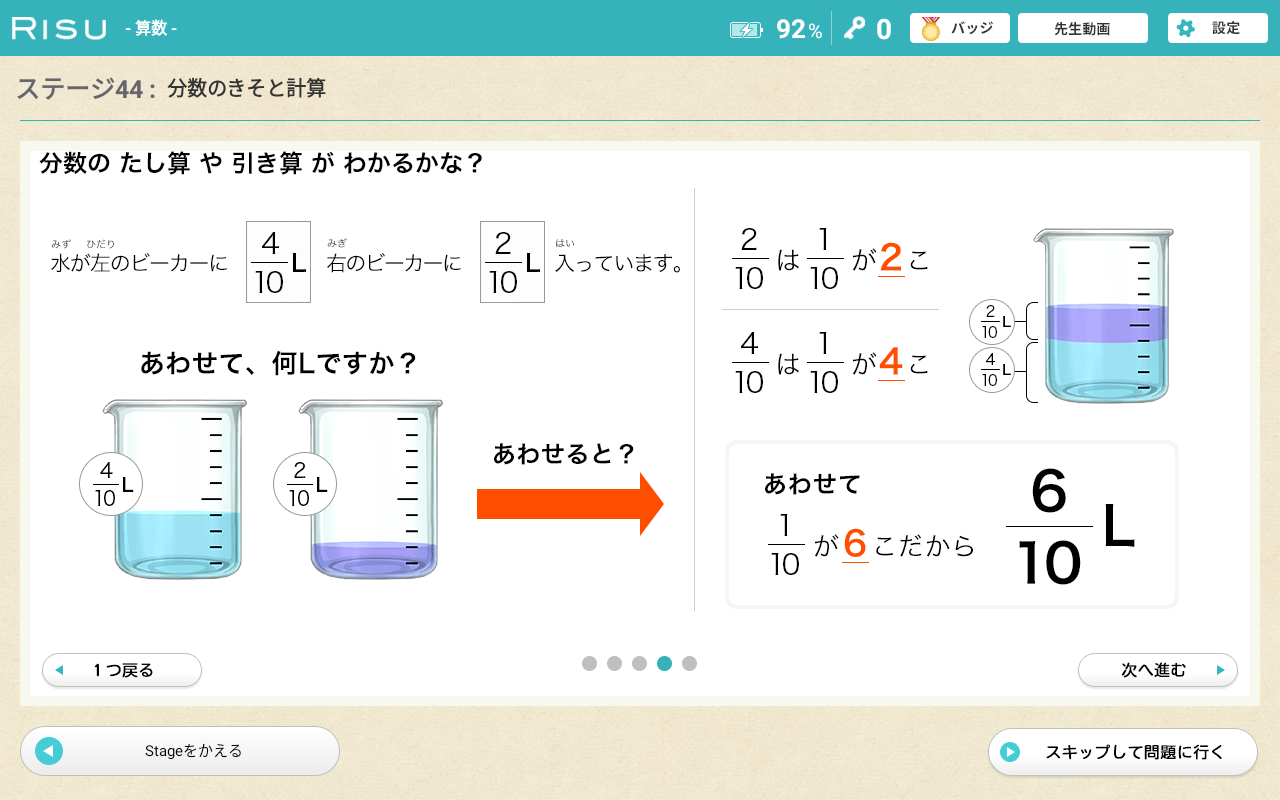
RISU算数には、図形問題や文章問題など幅広いレベルの問題が収録されており、
中学入試や算数オリンピック問題など、思考力を試す問題も多く含まれています。
進学塾に通っているお子さんであっても、計算力は高いのに文章を読み取るのが苦手で問われていることを正確に理解できないお子さんや、論理的に考えるのを苦手としているお子さんは多くいます。
分数は高学年以降、ほぼ全ての単元の文章問題で登場するため、応用力を試す問題では避けて通れません。
計算力だけでなく多くの文章問題に取り組み、論理的思考力を鍛えることが、算数の学力を伸ばすためには重要です。
特長3：視覚的に理解できる「解説動画」
RISU算数では、東京大学をはじめとするトップ大学生チューターによる解説動画が大人気。
特に視覚的イメージが重要になる分数ですが、RISU算数なら解説動画を見てお子さん一人で疑問を解決できます。
また定期的にチューターからの応援メッセージ動画を楽しみにされているお子さんもたくさんいらっしゃいます。
憧れの大学に通うお兄さんお姉さんからのメッセージは、学習へのモチベーションアップに最適です。
RISU算数には他にも、自動採点機能やメールで学習進捗をお知らせする機能など、保護者の方にも嬉しい機能が満載。共働きや小さいお子さんがいるなど、毎日忙しい親御さんも安心してお子さんの学習を見守ることができます。
視覚的に分数を理解することが大切
簡単な分数の学習は小2から始まります。
そのため、小2の学習から分数を視覚的に理解すること、通分や約分の学習に生かせるように九九を学習していくことを意識してほしいです。
そして、小3からは本格的に分数と割り算の学習が始まります。
割り算も学年が上がるにつれて立式や計算のイメージがより大切になります。
進んで復習に取り組み、コツコツと学習を積み重ねていきましょう。
RISU公式ブログでは、中学受験合格者・算数検定合格者・模試の成績優秀者など、RISU算数を活用した学習体験談を多数ご紹介しています。
お子さんの勉強の参考になる記事がきっと見つかるかと思いますので、ぜひ一度覗いてみてくださいね。
