算数は一つの単元の苦手を放置すると、必ずその後の単元でつまずいてしまいます。なるべく早く、正確に苦手をつぶしておきましょう。
分数のイメージを掴む

分数でつまずかないためには「分数のイメージ」を掴むことが大切です。
ただ、お子さんに「分数って何?」と聞かれたら、おうちの方はどう答えるでしょうか?
この章では、分数の意味を解説するとともに、分数のイメージを掴む大切さを解説します。
分数の意味は5つ
分数には5つの意味があります。
2/3を例に紹介します。
- 具体物を3等分したものの二つ分の大きさ
- 2/3L、2/3mのように測定したときの量の大きさ
- 1を3等分したものの二つ分の大きさ
- AはBの2/3 Bを1としたときのAの割合
- 整数の割り算2÷3の結果
分数に5つの意味があるのは驚きですね。
この5つの分数の違いが分からないと、特に文章題でのつまずきポイントになります。
お子さんが分数の学習で混乱するのも当然ですね。
小2で簡単な分数を習い、小学校3年生から分数の学習が本格的に始まりますが、①③のイメージが強すぎるため、小学校5・6年生で学習する④⑤の分数のイメージがないお子さんや親御さんは実は多いです。
割合を分数で表すことに抵抗を感じやすく、「1個のケーキを3等分するのが分数じゃないの? 1/3にあたるってどういこと?」「「どちらが分子と分母か分からない」となりがちです。
お子さんはどの分数でつまずいているのか、一度確認してみましょう。
分数の種類は3つ
分数には3つの種類の分数があります。
- 真分数(しんぶんすう)・・・1/2や3/5など、分子が分母より小さい分数。
- 仮分数(かぶんすう)・・・3/2、4/4、20/8など、分子が分母以上(分母より大きいか等しい)の分数。
- 帯分数(たいぶんすう)・・・1½、3¼など、 整数と真分数の和で表される分数。
お子さんはこの3つの分数を小4で学習します。
5つの分数の意味に加え種類が3つ。
お子さんが混乱するのも無理はありません。
お子さんの中には「整数や小数では、分数のように形が違うものは出てこなかった」「3と1/4ってどれくらいの大きさ?」など、?を抱え、解決しないまま学習が進んでしまっているお子さんもいます。
分数の意味や種類を確実に理解するには、分数のイメージを掴むことが大切になってきます。
視覚的に分数を理解し、イメージできるようにする
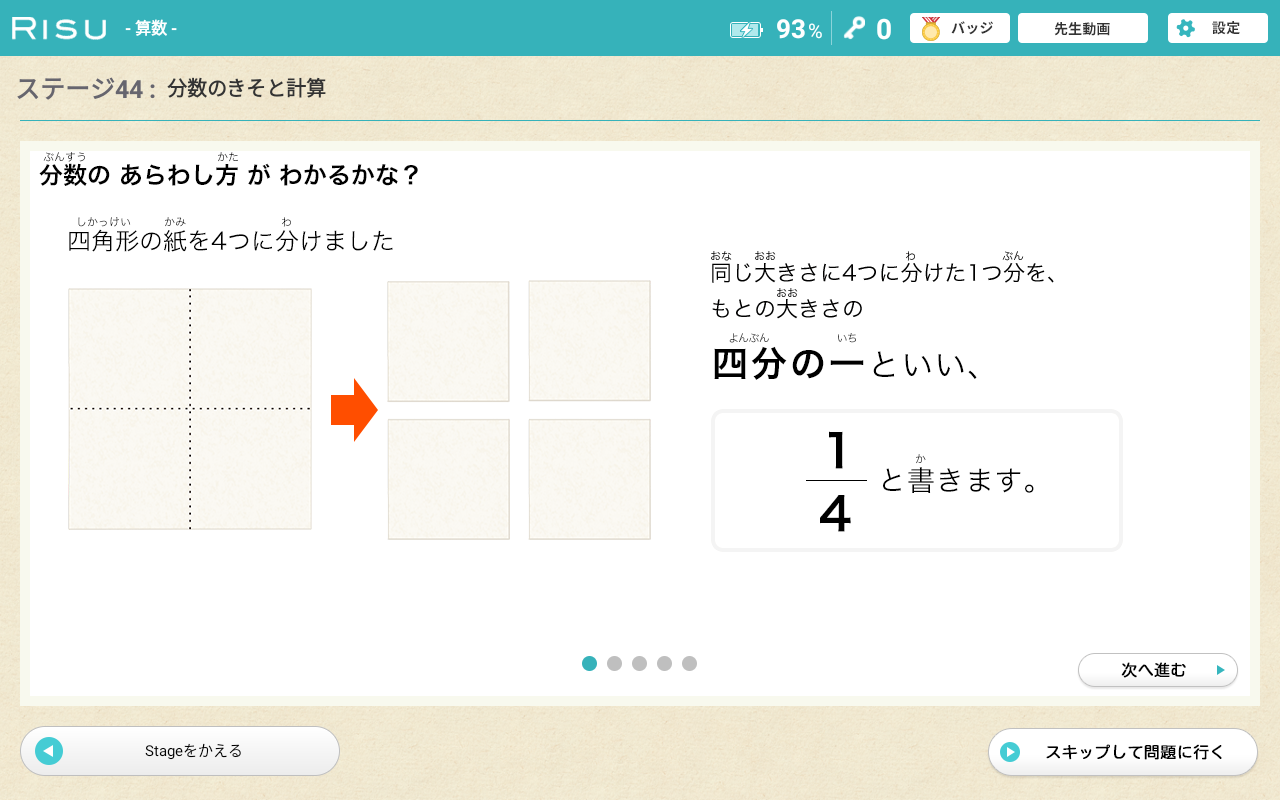
視覚的に分数を理解し、イメージを掴むことができると以下のことがわかるようになります。
- 分数の意味がわかる
- 分数の大小関係の比較ができる
- 分数と小数のつながりがわかる
「1/2と1/3はどちらが大きい?」という問題で、小5の正答率が49.7%であることが話題になりました。
(参考:分数の1/2と1/3では、どちらが大きい? 小5の正答率は49.7% https://bookplus.nikkei.com/atcl/column/091800417/111100048/)
この問題の間違えは、分数のイメージができず、数字の大きさに引っ張られるために起こります。
たしかに2より3の方が大きいのですが、分数では分子が同じ数の場合、分母の数が大きい方が小さい数になります。(分母が大きいほどより細かく分かれるからですね)
図で1/2と1/3を見ると、どちらが大きいかは一目瞭然です。
図やイラストなどで視覚的に理解して、分数をイメージできるようにしていきたいですね。
次に、「2/3と3/4ではどちらが大きいでしょうか?」という問題で考えてみましょう。
この問題は、分子も分母も異なる分数を比較するため、図のイメージだけでは危うい問題です。
実際に図で比較するとわずかに3/4の方が大きいです。
では、どれくらいの差でしょうか?
分子と分母が異なる分数は、小5で学習する通分を使って大きさを比較することもできます。
2/3⇒8/12
3/4⇒9/12
また、分数を小数にして比較する方法もあります。
2/3=2÷3=0.66・・・
3/4=3÷4=0.74・・・
図で比較したときのわずかな差が、数字としてはっきり表れました。
このように、図やイラストを活用して視覚的に分数を理解していくと、通分の意味や分数と小数のつながりなども理解しやすくなります。
家庭で日常的に分数に触れる
お子さんが分数を理解しにいく原因はもう一つあります。
それは、分数がお子さんの日常で使われていないことです。
大人の世界では分数を使うのが当たり前でも、経験の少ない子どもにとってはそうではありません。
ですから、親御さんは日常の生活でお子さんがなるべく分数にふれるように工夫しましょう。
例えば、食べ物などを分ける場面では「半分に分けて」や「4等分に分けて」など、分数につながる言葉を使っていきましょう。
カレンダーを使った「6月で1年も1/2(半分)だ」「12月も1/3が過ぎた」などの言葉かけもよいですね。
小6では時間を分数で表す学習があり、図にある時計を9/12や3/4と見たりする力が必要です。
分数の計算のつまずきポイント4つ
分数の計算は手順が多く、分数が苦手になる原因の一つです。
この章では、分数の計算でつまずくポイントを4つに分けて解説します。
「【小学生】算数の計算ミスがなくならない!7つの原因と対策方法を徹底解説(学び相談室)」
通分
通分とは、2つ以上の分数の分母を同じ数にそろえることです。
通分により、分数の足し算・引き算を簡単に行うことができるわけですが、なぜ1/2+1/3のように分母が異なると計算できないのでしょうか?
これも図で表すとよくわかります。
先ほどの1/2と1/3の図を合わせた(足し算した)図が以下のものです。
図では大きさがわかるものの、これがいくつを表すのか定かではありません。
そこで、通分をする必要が出てきます。
お互いの分母を最小公倍数の6にそろえ、1/2は3/6に。1/3は2/6に通分します。
すると1/6が5個あり、答えは5/6になることがわかります。
通分をして同じ分母の6にする意味も図からわかるのではないでしょうか。
このように、分数のイメージができていると、分数の計算でつまずく可能性も低くなります。
通分ができるようになるためには、九九や公倍数・最小公倍数の定着が重要です。
「小3の子どもへの分数の教え方を知りたい!家庭で簡単にできる方法はありますか?(学び相談室)」
約分
約分とは、分数の分母と分子を同じ数で割って、分母をより小さくすることです。
分数の計算の答えは、約分をして分母の数を最小にすることが求められます。
では、なぜ約分をして、分母の数を小さくするのでしょうか?
答えは、分母が大きい分数より分母が小さい分数の方が、分かりやすいからです。
例えば35/145と1/3は同じ大きさですが、分母が小さい1/3の方が大きさをイメージできます。
算数では答えをよりシンプルに表すことが求められているため、答えを分数で出す場合は約分が必要になるのです。
約分ができるようになるには、九九と約数・最大公約数の理解と定着が重要です。
逆数
逆数とは、ある数を掛けると1になる数です。
2/3の逆数は3/2です。(つまり分母と分子を入れ替えた数)
逆数は小6で学習します。
逆数を学習すると、整数や小数も分数に変換できます。
例えば、3(3/1)の逆数は1/3であり、0.7(7/10)の逆数は10/7となります。
また、分数の割り算では割る数の逆数をかける方法を学習します。
2/5 ÷ 3/7では、割る数の3/7の逆数である7/3を2/5にかけて答えを求めます。
詳しい解説は割愛しますが、計算方法を形式的に理解し、「なぜこの式になるのか?」「なぜこの計算過程なのか?」を考えられないお子さんは多いです。
分数の計算でつまずく原因にもなり、算数の思考力が身に付かない原因にもなります。
分数以前のつまずき
本格的な分数の計算は整数・小数の計算の後に学習します。
お子さんは整数や小数で学習したことを生かして、分数の計算を学習していきます。
もし分数の計算ができない原因に、整数や小数の四則計算でつまずいている可能性があります。
特に小2で学習する九九は、通分や約分に必要不可欠の知識です。
また、分数は小数と関連づけて学習が進みます。
4/5から0.8に変換したり、0.75から3/4に変換したりお互いに変換し合う関係にあります。
そして、1÷3=0.333・・・のように割り切れない割り算の答えも、分数ならば1/3と表せます。
分数の計算をマスターするには、整数や小数の確実な理解と、分数のイメージが大切です。
小1や小2での基礎固めや復習に進んで取り組み、学習を積み重ねていく必要があります。
分数を得意にするなら「RISU算数」がおすすめ

算数の家庭学習には、算数専用タブレット教材の「RISU算数」がぴったりです。
特長1:「無学年制」で一人ひとりにピッタリのカリキュラム

RISU算数では無学年制カリキュラムを採用。
学年を超えてどんどん先取り学習を進めることも、
つまずいた分野で学年を遡って復習することもタブレット一台で完結します。
またRISU算数ではデータに基づき、お子様の学力に合わせた出題がなされるため、
難しすぎて勉強が嫌いになってしまうということや、簡単すぎて退屈するということもありません。
つまり、解き甲斐があり楽しい問題がつづくため学習習慣が自然に身につき、着実に基礎力を固めることができるのです。
特長2:丁寧な解説で分数のイメージが身に付く

進学塾に通っているお子さんでも、計算力は高いのに文章問題は苦手というお子さんは多いです。
これは分数のイメージを掴めないままでいることが原因。
RISU算数では、図や具体例を用いてイメージを掴むことを重視した解説が特長。
計算力だけでなく算数全体を伸ばすことができます。
またRISU算数には、図形問題や文章問題など幅広いレベルの問題が収録されており、中学入試や算数オリンピック問題など、思考力を試す問題も多く含まれています。
基礎を固めたいお子さんも、ハイレベルな問題に挑戦したお子さんも、ぴったりの問題に挑戦することができます。
特長3:分かりやすい「解説動画」

RISU算数では、東京大学をはじめとするトップ大学生チューターによる解説動画が大人気。
分からない問題も、解説動画を見てお子さん一人で解決することができます。
また定期的にチューターからの応援メッセージ動画を楽しみにされているお子さんもたくさんいらっしゃいます。
憧れの大学に通うお兄さんお姉さんからのメッセージは、学習へのモチベーションアップに最適です。
RISU算数には他にも、自動採点機能やメールで学習進捗をお知らせする機能など、保護者の方にも嬉しい機能が満載。共働きや小さいお子さんがいるなど、毎日忙しい親御さんも安心してお子さんの学習を見守ることができます。
分数の苦手を克服するには
分数が苦手な原因は、分数のイメージの掴みづらさと計算の複雑さにあります。
本記事を参考に、お子さんが分数を視覚的に理解できるように心掛けていきましょう。
また、分数の計算では通分や約分、逆数の概念をしっかり押さえ、整数や小数の基礎を復習することが欠かせません。
お子さんの実態に合わせて復習を積み重ねていきましょう。
RISU利用者レビューでは、RISU算数をご利用いただいている保護者様の声をご紹介しています。
中学受験で志望校合格、大手塾模試で成績が大幅アップ、家庭学習の質が上がった、など皆様の参考になるリアルな体験談が多数。
RISU公式ブログでは、算数オリンピックメダリストや先取り学習での算数検定合格者、大手塾主催模試での成績優秀者など、お子様の声を中心にご紹介しています。
ぜひ一度お読みください!