小3の子どもは算数の図形問題が苦手なのですが、どうすれば克服できるでしょうか？中学受験も考えているので不安です。また下に5歳の妹もいますが、この先図形問題が得意になるために幼児期に取り組むとよいことはありますか？

図形問題でつまずく理由

図形問題でつまずく理由は、大きく4つあります。

1.図形をイメージする力の不足

1つ目は、図形をイメージする力の不足です。

たとえば、「サイコロの展開図を見て、向かい合う面はどれとどれか答えなさい」という問題では、立体図形の展開図をイメージできずにつまずくお子さんが多くいます。
平面（紙に描かれた展開図）から立体（実際のサイコロ）への変換するには、イメージする力が必要です。

また、「L字型の図形の面積を求めなさい」といった、複雑な形の面積を求める際に、形の分割がイメージできないお子さんもいます。

こうしたイメージ力は、手を動かして図形に触れる機会の積み重ねで養われます。

2.図形の基礎用語や公式の理解があいまい

2つ目は、図形の基礎用語や公式を十分に理解できていないことです。

読者の皆さんは「角」と「頂点」の違いを説明できますか？
この2つの違いを説明できるお子さんは実は少なく、大人でも正しく説明するのは難しいです。

「角」は、2本の線分や直線、半直線が1点で交わるとき、その交わった部分にできる「開き」のことを指します。
「頂点」は、角を作る2本の線分や直線が交わっている「1点」のことです。

図形問題では「角と頂点」のように、似ているようで意味が異なる言葉が数多く登場します。

• 辺と面
• 直角と垂直
• 半径と直径
• 線対称と点対称
• 合同と相似

こうした図形の基礎用語をあいまいに理解していると、つまずきの原因になります。

3.公式を丸暗記している

図形問題には面積や体積を求める公式が数多くあります。

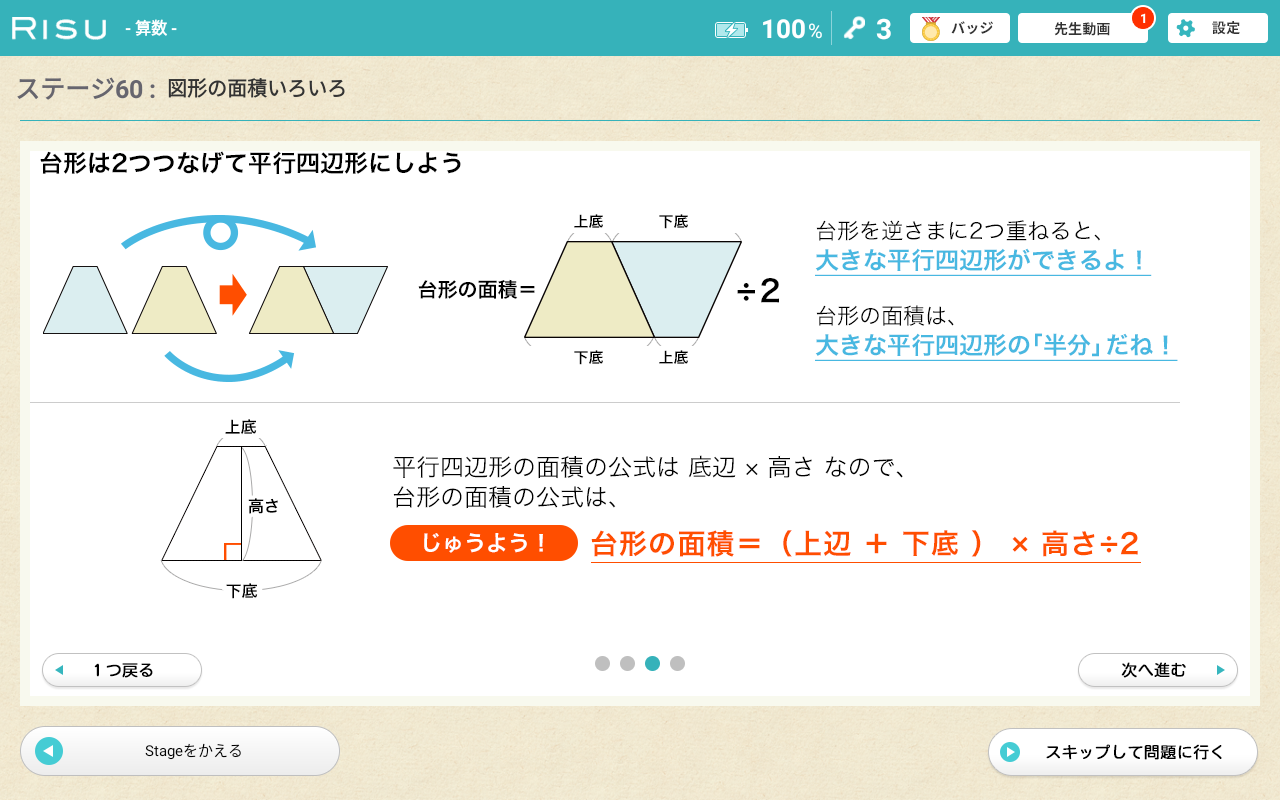
三角形の面積を求める公式は「底辺×高さ÷2」ですが、なぜこのような公式になるのでしょうか？
その理由は、以下のように説明できます。

①面積を求める三角形と合同な三角形をもう1つ作って、向かい合わせに並べると、平行四辺形ができます。
②平行四辺形の面積は「底辺 × 高さ」。
③もとの三角形はその半分なので、面積は「底辺 × 高さ ÷ 2」となります。

しかし公式の意味を理解せずただ暗記してしまうと、少し複雑な応用問題になったとたんに、どの公式をつかえばいいのか分からなくなってしまいます。

4.図形を言語化する力の不足

図形問題でつまずく4つ目の理由は、図形を言語化する力が不足していることです。

たとえば、図形に苦手意識をもつお子さんには、長さや重さを問われているのに「大きい・小さい」でしか答えられなかったり、「m」「㎠」「°（度）」などの単位を使って正確に表現できなかったりすることが多いです。

また、図形の基礎用語を使って説明できないこともあります。

「おにぎりのような形はなぜ三角形ではない？」という問いに対して、「三角形に見えないから」「形が違う」といった視覚的な印象だけで答えてしまうと、抽象的な内容が増える中学年以降の図形問題につまずきやすくなります。

「三角形とは、3本の直線で囲まれている形を指す。おにぎりは直線で囲まれていないため、三角形とは言えない」と、低学年のうちから図形の用語を用いて具体的に説明できるようになることが大切です。

図形問題の苦手を克服する方法

ここからは図形問題の苦手を克服する方法を発達段階別に解説します。

幼児期の図形対策

幼児期は、図形にたくさん触れて直感的・視覚的に理解していくことがポイント。

以下のようなご家庭での取り組みが効果的です。

• 折り紙・切り紙
• お絵描き
• 積み木・ブロック・立体パズル
• 空き箱で工作

幼児期の図形対策では、遊びの延長で図形に親しむ環境づくりが大切です。

「三角（四角・丸）に切れるかな？」「ブロックで車を作れるかな？」と、積極的に声をかけ、お子さんが図形を楽しめるようにしましょう。

「幼児への算数の教え方は？算数センスを磨く学習法を知りたい（学び相談室）」

低学年（小1～小3）の図形対策

低学年は、感覚的な理解から具体的な理解へと移行していく時期。
これまで遊びの中で触れていた形を「図形」として学んでいきます。

1年生・2年生では、主に以下を学習します。

• 図形の名前や特徴
• 形の違い
• 三角形・四角形などの基本的な形を見分ける
• 辺・頂点といった用語

ものの大きさや長さ比べ、簡単な図形遊びを通して、イメージ力を育てることがポイントです。

3年生になると、図形の学習が本格化します。

• 二等辺三角形・正三角形・円・球など、より具体的な図形の性質
• コンパスや三角定規の活用
• 円や直線
• 角度の概念

この時期は、図形の性質を理解し、基本的な作図をできるようにすることが大切です。

図形の性質とは、図形ごとに備わっている特徴や、図形同士に共通する法則や関係性のこと。
たとえば、三角形には以下のような性質があります。

• 三角形の内角の和は必ず180°になる
• 2つの辺の長さの和は、残り1つの辺の長さより大きい（成立条件）
• 辺の大小関係は、その向かい合う角の大小関係と一致する
• 外角は、それと隣り合わない2つの内角の和に等しい

3年生以降の図形学習では、さらに図形の性質が多く出てきます。
「二等辺三角形ってどんな形？」「正方形の特徴は？」といった問いかけを、ご家庭でも意識的に行いましょう。

また、この時期はコンパスや三角定規の使い方に苦戦するお子さんも多く見られます。
正しい方法で何度も作図することで、自然とコンパスや三角定規に慣れていくようにしましょう。

高学年（小4～小6）の図形対策

高学年では、図形問題の学習内容がより抽象的になります。

そのため、形をイメージしたり、図形を言葉で表現したりする力がより一層必要になります。

抽象度が高くなり始める4年生では、以下の内容を学習します。

• 平行四辺形・台形などの学習
• 立体図形の基礎
• 分度器で角度を測る
• 見取り図や展開図を作る
• 平面図形（長方形、正方形）の面積を求める

4年生からは面積を求める学習が始まります。
計算力も大切ですが、「なぜこの公式を使うのか？」を理解することが重要です。
この公式の意味理解は、5・6年生の学習にもつながります。

また4年生は、平面図形の作図や、直方体・立方体などの立体図形が登場。
コンパスや分度器を使ったり、立体図形を触って特徴を探ったり、手を動かす学習がポイントになるため、幼児期に培った図形の感覚的な理解がここで活かされます。

「小4の「算数の壁」をクリアできるか不安。小4で算数が苦手にならないための対策はありますか？（学び相談室）」

5年生では、さらに複雑な内容を学びます。

• 角柱・円柱などの立体図形の見取り図・展開図・体積計算
• 合同な図形の作図
• 正多角形の内角の和の計算
• 円周率を使った円の面積や円周の長さの計算

一気に難易度が上がった印象がありますね。
とはいえ、これまでの知識を活用して計算する内容が中心です。
復習しながら新しい内容を学習していきましょう

お子さんが「分からない」「難しい」と感じたときは、「前の学年の内容を見てみよう」「復習しよう」と声をかけてあげてください。

最高学年の6年生では、図形問題の総まとめと中学校で学ぶ内容の基礎を学習します。

• 円の面積や角柱・円柱の体積
• 図形の拡大・縮小（相似の基礎）
• 縮図や拡大図の考え方

6年生で図形問題に苦手意識がある場合は、3年生の内容まで戻って復習するのがおすすめです。
図形の特徴、基礎用語、面積や体積の公式といった基本的な内容をもう一度丁寧に積み上げることで、6年生での学習も理解しやすくなります。

「中学受験の算数で基礎固めはいつから始めるべき？家庭でできる学習方法を教えてください。（学び相談室）」

中学受験の図形問題対策

最後に、中学受験における図形問題の対策について解説します。

作図をたくさんする

中学受験の図形問題で、特に得意・不得意の差が大きいと言われているのが作図問題です。

ポイントは以下の3つです。

• 基本操作をマスターする
• 問題文の条件を正確に読む
• 図形の性質を活用できるようにする

コンパスや定規の使い方に加え、垂直二等分線、角の二等分線、円の作図、決まった長さの線分といった作図の基本操作を必ずマスターしましょう。

そのときに必要なのが、図形の性質の理解です。
図形の性質を理解していないと、作図ができません。

また、作図の問題文の条件を正確に読む習慣も大切です。
特に「定規とコンパスのみ」「Aの三角形は直角二等辺三角形です」といった指示や条件に注意しましょう。

角度を問うような問題では分度器を使わずに、条件を頼りに論理的に答えを導き出す力が求められます。

図形を言葉で説明する

中学受験の図形問題では、図形の意味や仕組み、補助線を引く意図などを言語化して説明する力が必要です。

低学年のうちから「長い・短い」「大きい・小さい」「重い・軽い」「広い・狭い」などの言葉を正確に使い、図形を言葉で説明する練習をしていきましょう。
図形をただ見るだけではなく、言語化することで思考が整理され、記憶にも残りやすくなります。

また、問題の図に補助線などを書くと同時に、そこからわかったことを言葉や記号で書き込みます。
「ここは同じ長さ」「AとBの角度は同じ」と情報を整理すると、答えの道筋が見えてきます。
日頃の学習から図形を言語化するように意識し、理解を深めるようにしていきましょう。

図形問題の基本的な解法を覚える

中学受験の図形問題では、頻出問題の対策がとても大切です。
以下のステップを踏んで何度も問題を解き、解法を覚えていきましょう。

• 図を描いて条件を整理する習慣をつける
• 問題文の条件や与えられた数値を図に書き込み、視覚的に整理する
• 長さや角度、等しい部分を図に明記し、補助線を積極的に引く
• 合同・相似・等積移動など、図形問題でよく使う考え方を場面ごとに使い分けて練習する

図形問題の解法で特に重要なのは、いきなり解き方を考えず条件を整理することです。

受験問題では「ひらめきが重要」といった言葉がよく見受けられます。
しかし、「ひらめき」は、基本的な解法の習得と、多くの問題演習を通して蓄積された結果として身につくものです。
「センス・感覚」に頼るのではなく、正しい学習を積み重ねてひらめけるようになりましょう。

図形問題の苦手克服なら「RISU算数」がおすすめ

図形問題を苦手克服には、算数専用タブレット教材の「RISU算数（幼児には「RISUきっず」）」がぴったりです。
算数の図形問題が得意になるRISU算数の特長3つをご紹介します。

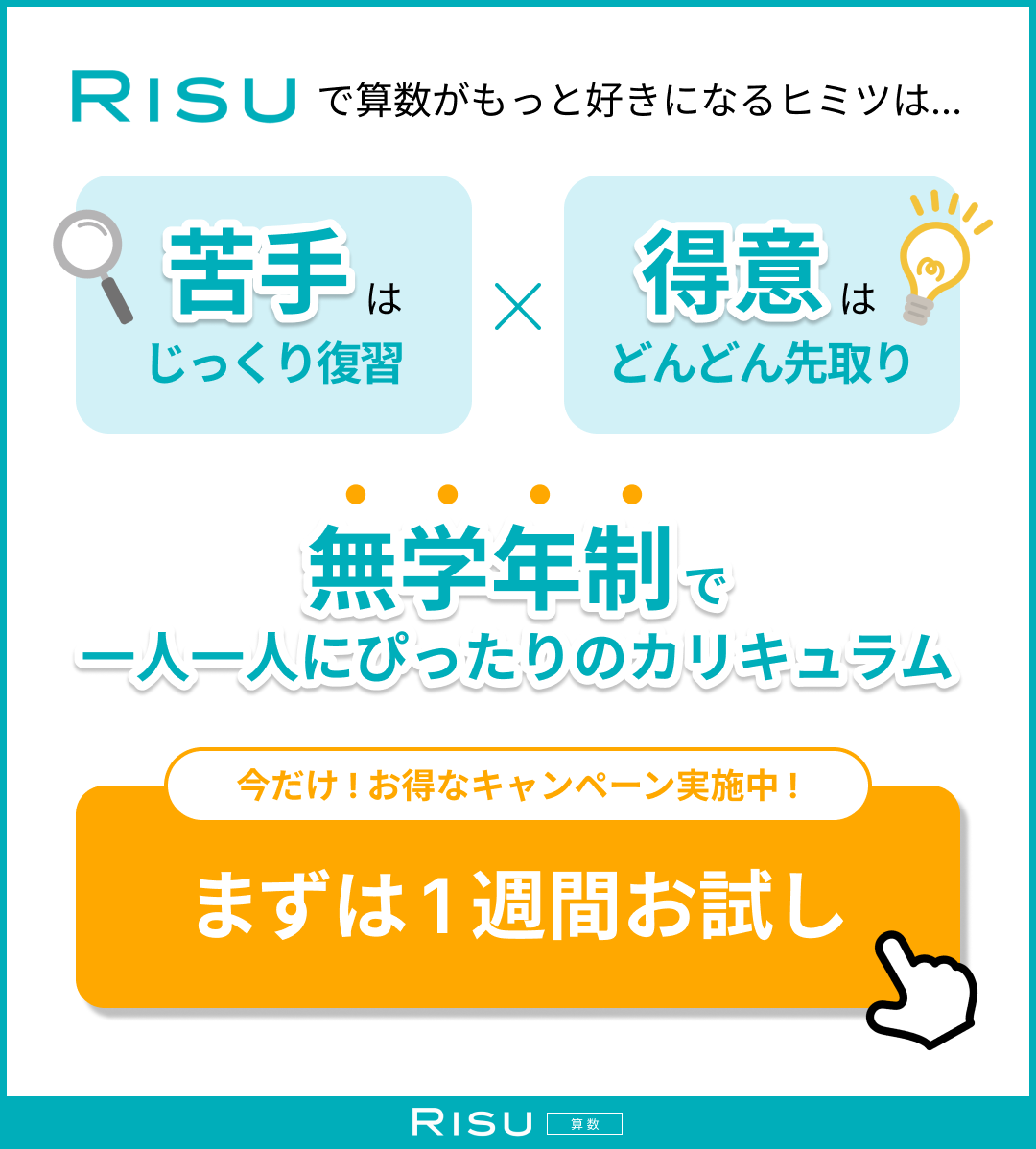
特長1：「無学年制」で一人ひとりにピッタリのカリキュラム

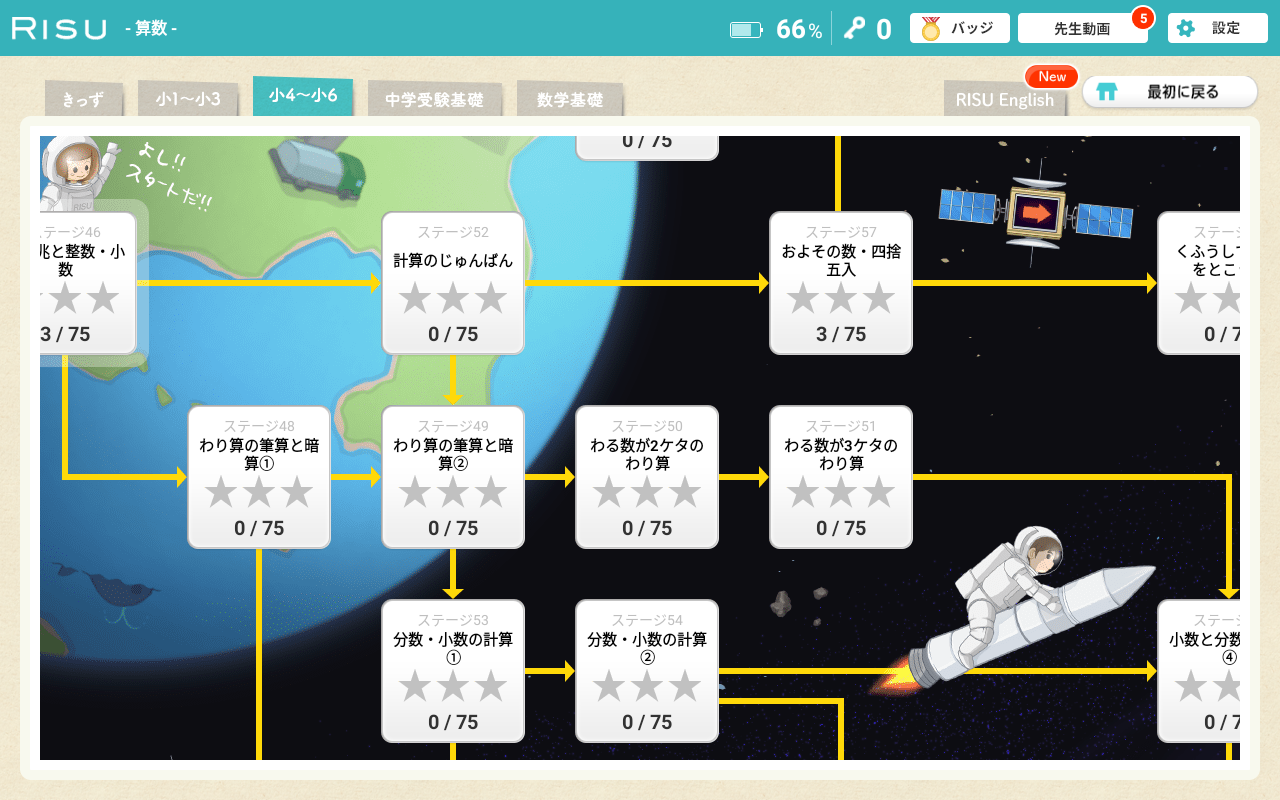
RISU算数では無学年制カリキュラムを採用。

学年を超えてどんどん先取り学習を進めることも、
つまずいた分野で学年を遡って復習することもタブレット一台で完結します。

またRISU算数ではデータに基づき、お子様の学力に合わせた出題がなされるため、
難しすぎて勉強が嫌いになってしまうということや、簡単すぎて退屈するということもありません。
つまり、解き甲斐があり楽しい問題がつづくため学習習慣が自然に身につき、着実に基礎力を固めることができるのです。

特長2：図形問題や文章問題で思考力が身に付く

RISU算数には、図形問題や文章問題など幅広いレベルの問題が収録されており、
中学入試や算数オリンピック問題など、思考力を試す問題も多く含まれています。

計算塾や進学塾に通っているお子さんであっても、
計算力は高いのに文章問題や図形問題が苦手だったり、論理的に考えるのを苦手だったりするお子さんは多くいます。

RISU算数では、基礎的な計算問題からハイレベルな文章問題まで、算数の学力をバランスよく伸ばすことができます。

特長3：分かりやすい「解説動画」

RISU算数では、東京大学をはじめとするトップ大学生チューターによる解説動画が大人気。
分からない問題も、解説動画を見てお子さん一人で解決することができます。

また定期的にチューターからの応援メッセージ動画を楽しみにされているお子さんもたくさんいらっしゃいます。
憧れの大学に通うお兄さんお姉さんからのメッセージは、学習へのモチベーションアップに最適です。

RISU算数には他にも、自動採点機能やメールで学習進捗をお知らせする機能など、保護者の方にも嬉しい機能が満載。共働きや小さいお子さんがいるなど、毎日忙しい親御さんも安心してお子さんの学習を見守ることができます。
RISU算数では、4歳から取り組んでいただける未就学児向けの問題もあり、幼児教育にお使いいただくことができます。
イラストやアニメーションを使った解説で、未就学のお子様でも楽しく取り組んでいただける内容になっております。

図形問題の苦手を克服する方法まとめ

図形問題では、「センス・感覚」が問われがちです。

しかし、「センス・感覚」を求めて、幼児期から図形に触れさせたり、工作体験をしたりするだけでは不十分です。

図形の基礎用語や性質といった基本の理解を第一に、感覚的な理解だけではなく、言語化を通してバランスよく図形の理解を深めていきましょう。

RISU利用者レビューでは、RISU算数をご利用いただいている保護者様の声をご紹介しています。
中学受験で志望校合格、大手塾模試で成績が大幅アップ、家庭学習の質が上がった、など皆様の参考になるリアルな体験談が多数。

またRISU公式ブログでは、算数オリンピックメダリストや先取り学習での算数検定合格者、大手塾主催模試での成績優秀者など、お子様の声を中心にご紹介しています。

ぜひ一度お読みください！