ポイントは図や表を用いてイメージを持つこと。
その上で公式を覚え、問題演習を繰り返しましょう。
つるかめ算の解法
例題1
「つる」と「かめ」があわせて10います。足の合計本数は32本です。かめは何匹いますか？
ポイント
- つるの足 2本
- かめの足 4本
誰でもわかるとは思いますが、これがポイントです。
1.表で考える
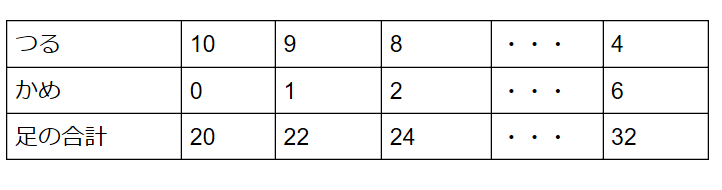
全部つるだとすると足の数は20本。
この方法だと上の図のように「つるが10、かめが0だとすると20本」「つるが9、かめが1だとすると22本」というように順に調べていくことができます。
しかし、数が多いといつまでも書き続けるわけにはいかないので、足の合計本数が等差数列になっていることを利用するといいです。
足の合計数が32本になる時は、
（32-20）÷2＝6
なので、亀が6匹いるということになります。
10-6=4で、つるは4羽となります。
この場合は、「つる1羽をかめ1匹に変身させるごとに足の合計が2ずつ増えていく」ことを利用して考えています。
全部をかめだと考えたら、「かめ1匹をつる1羽に変身させるごとに足の合計が2ずつ減っていく」ことを利用して考えていくことになります。
2.式で考える
全部をつるだとした場合の式
（合計の足数-つるのあし×合計の頭数）÷（かめの足-つるの足）
となっています。
さきほどの例題をこちらの式にあてはめてみましょう。
（32-2×10）÷（4-2）
＝12÷2
＝6
かめの数が出ましたね。
10-6＝4
こちらがつるの数です。
つる4羽
かめ6匹
また、全部をかめだとした場合の式
（かめの足×合計の頭数-合計の足数）÷（かめの足-つるの足）
となっています。
同じように例題を式にあてはめてみましょう。
（4×10-32）÷（4-2）
＝8÷2
＝4
つるの数が出ましたね。
10-4＝6
こちらがかめの数です。
ここまでで、なにかきづきませんか？
そうです。
全部をつると考えた場合はかめ、全部をかめと考えた場合はつるの頭数が先にわかりますよね。
例題ではかめの数が答えとして聞かれていたので、全部をつると考えるのが最適だといえるでしょう。
つるかめ算のパターン
つるかめ算には様々なパターンがあります。
1円玉と5円玉が合わせて〇枚あり、その合計金額は〇円です。1円玉と5円玉の枚数をそれぞれ答えなさい。
〇km離れた目的地に徒歩とバスで行きました。徒歩は時速〇km、バスは時速〇kmで、目的地まで〇分かかりました。バスには何分乗っていたでしょうか。
速さや割合などさまざまな問題があります。
（例題2）
1個80円のりんごと1個50円のみかんをあわせて11個買ったら、代金は700円でした。
みかんは何個買いましたか？
この場合、どちらを最大数買ったと考えればいいでしょうか。
みかんの数を知りたいので、りんごですね。
先ほどの式にあてはめてみましょう。
値段が安いみかんをつる、値段が高いりんごをかめと考えます。
すると、使う式は全部をかめだとした場合の式です。
（かめの足×合計の頭数-合計の足数）÷（かめの足-つるの足）
今回の問題用に直すと
（りんごの値段×合計の個数-代金）÷（りんごの値段-みかんの値段）
計算してみましょう。
（80×11-700）÷（80-50）
＝180÷30
＝6
よってみかんは6個です。
つるかめ算は中学校で習うことになる連立方程式の基礎にもなっています。
小学生のうちにマスターしておくことをおすすめします。
中学受験を見据えるなら小学3年生のうちから始めるべきです。
ぜひこちらのページもご覧ください。
3年生からの受験準備
「RISU算数」なら中学受験算数の基礎が身につく
算数専用タブレット教材の「RISU算数」は、4歳から中学受験基礎（さらに中学数学基礎）の問題まで約10000問を収録。
学校の内容から中学受験対策レベルまで、無理なく自然に算数力が身につきます。
「つるかめ算など中学受験塾で習う算数の予習や復習にぴったり」
と、多くの中学受験を目指すご家庭に活用いただいています。
つまずきなく着実に算数力が身に付くRISU算数の3つの特長をご説明します。
1.スモールステップ＆無学年制カリキュラム
4歳から中学受験基礎（さらに中学数学基礎）の問題まで約10000問を収録。
スモールステップで少しずつ先に進むので、つまずきにくく自然にステップアップしていけます。
またRISU独自の無学年制カリキュラムを採用。
学年を超えてどんどん先取り学習を進めることも、つまずいた分野では学年を遡って復習することもタブレット一台で完結します。
紙のテキストのように何学年分も用意する必要はありません。
また「算数検定マスター判定」によって、算数検定の受検可能級をお知らせ。
実際より上の算数検定の階級に合格することで、受検費用が0円になるおトクなサポート制度もあります。
中学受験に向けた先取り学習の定着度や、分野別の得意不得意の分析に算数検定を活用できます。
参照サイト：RISU算数が算数検定対策になる！助成金で検定料を無料にする方法も解説
2.データ分析で一人ひとりにベストな問題が届く
RISU算数では、タブレットを通じて利用者ひとりひとりの学習データを常に収集・分析。
得意分野・苦手分野を把握し、利用者の実力に合った問題となるよう、お子様に合わせて問題が変わっていきます。
難しすぎてついていけなくなったり、簡単すぎて飽きてしまうこともないのです。
一人ひとりのペースに合わせて、効率よく実力を伸ばすことができるのがRISU算数の大きな特長です。
ほかにもお子さんにもおうちの方にも嬉しい機能がたくさん。
くわしくはこちらをご覧ください。
3.自動採点機能つき ゲーム感覚でどんどん進む
タブレット教材のRISU算数なら問題を解いたら自動採点機能でその場ですぐに採点。
おうちの方が丸つけする必要がないので、お子さんだけでどんどん学習をすすめることができます。
テンポよくステージをクリアしていくことで、まるでゲームを攻略するように楽しんで進めることができます。
RISUのタブレット教材ならば飽きることなく、楽しく学習できます。
また、忘れてしまいがちなタイミングでの復習と間違いが多かった問題の復習をミックスして復習を自動出題し、学習の定着を図れます。
さらに、つまづきを感知してフォローアップし、やる気や学習習慣づけまでサポートしてくれます。
親御さんが細かく口を出す必要が無いので、親子の丁度いい距離感を保つことができます。
RISU算数を活用した中学受験のリアルな体験談＆口コミはこちらの記事でご紹介しています。
まとめ
今回はつるかめ算について解説をしました。
RISU算数の中学受験基礎クラスでは他にも、旅人算や規則性の問題といった中学入試頻出算数について基礎をしっかり学べます。
難しいと感じられがちな算数ですが、分かることが増えるとゲームのように楽しんで解けるようになりますよ。
ぜひ一つひとつ「わかる」「できる」を積み上げ、楽しみながら中学受験算数をマスターしてみてくださいね！
RISU公式ブログでは、成績優秀者へのインタビュー、算数検定合格者、中学受験合格の声をご紹介しています。
RISU利用者のリアルな体験談をぜひお読みください！
